Solargewinne versus Wärmebrücke
- 01
- Úno
Solargewinne und Wärmebrücke spielen in der Energiebilanz eines Passivhauses eine bedeutende Rolle. Hier sollen die Details der Fensterlaibung beschrieben und der Einfluss verglichen werden, den der Abstand des Fensters von der Sichtfläche der Fassade auf die Wärmebrücke und auf die Solargewinne hat, bzw. welche Gewinne wir aufgrund der Beschattung durch Mauerecken verlieren.

Sonnenenergie und Wärmegewinne
Auf die Erdatmosphäre trifft eine Energie von ungefähr 1 373 W/m2. Leider haben wir diese Energie nicht im vollen Umfang zur Verfügung. Ein Teil verliert sich in der Atmosphäre. Je länger die zurückgelegte Strecke der Sonnenstrahlen durch die Atmosphäre, desto größer ist der Energieverlust. Im Winter geht aufgrund des niedrigen Sonnenstandes am Horizont also mehr Energie verloren als im Sommer. Wenn die Sonne 15° über dem Horizont steht, dann könnte die auf die senkrechte Ebene der Verglasung einfallende Sonnenenergie ca. 560 W betragen. Nach innen dringt nur ein Teil dieser Energie.
Wir haben einen Fall ausgewählt, in dem die Ablenkung der Strahlen von der Verglasungsebene 45° und die Lichtdurchlässigkeit der Verglasung 0,5 (Solarkoeffizient) ist. Um diese Energie mit den durch die Wärmebrücke verursachten Verlusten in der Fensterlaibung zu vergleichen, müssen wir den durchschnittlichen Wert dieser Leistung pro Monat verwenden. In Prag gibt es im Januar (laut TZB-Info) z.B. nur 43 Sonnenstunden.
In Tabelle 1 ist aufgeführt, wie in diesem konkreten Fall die Verwertbarkeit der Solarenergie sinkt, wenn nach und nach alle relevanten Einflüsse berücksichtigt werden. Selbstverständlich handelt es sich um Werte, die in unserem konkreten Fall gelten.
| Solarkonstante: | 1373 W/m2 |
| Energie, die bei einer Sonnenhöhe von 15° über dem Horizont auf die senkrechte Ebene der Verglasung einfällt | 560 W/m2 |
| Ablenkung der Strahlen um 45° von der Verglasungsebene | 396 W/m2 |
| Solarkoeffizient 0,5 | 198 W/m2 |
| Durchschnittliche Leistung für Prag im Falle von 43 Sonnenstunden im Januar | 11,4 W/m2 |
| Stufe der Ausnutzung der Wärmegewinne 0,7 | 8,01 W/m2 |
Die Energie, die in den Innenraum dringt, kann nicht in vollem Umfang genutzt werden. Es ist daher erforderlich, diese Energie weiter zu verarbeiten. Ein Vorteil ist, wenn das Bauwerk große Wärmespeicherfähigkeiten aufweist. Dies wird in der Stufe der Ausnutzung von Wärmegewinnen berücksichtigt. Auch ein flexibles Heizsystem ist von Vorteil. Beginnt die Sonne in einen Raum eines Passivhauses mit niedriger Wärmespeicherfähigkeit und langsam wirkendem Heizsystem zu scheinen, dann erhöht sich die Raumtemperatur so sehr, dass der Benutzer wahrscheinlich das Fenster öffnet, und zwar auch dann, wenn die Außentemperatur um die Null Grad liegt.
Zudem ist die Tatsache zu berücksichtigen, dass es notwendig ist, im Sommer übermäßige Solargewinne zu vermeiden.
Wärmebrücke in der Fensterlaibung
Als ein praktisches Beispiel habe ich ein Fenster des Typs Slavona PROGRESSION ausgewählt, das in einem Mauerwerk aus Kalksandsteinen mit Wärmedämmung durch ein Kontaktwärmedämmungssystem eingefasst ist. Die sichtbare Fläche des Rahmens auf der Außenseite ist minimal und zusätzlich aus einem beständigeren Material, wir können also das Fenster nahe zur Sichtfläche der Fassade einfassen und müssen keine übermäßige Degradierung der Oberfläche durch Umwelteinflüsse befürchten.
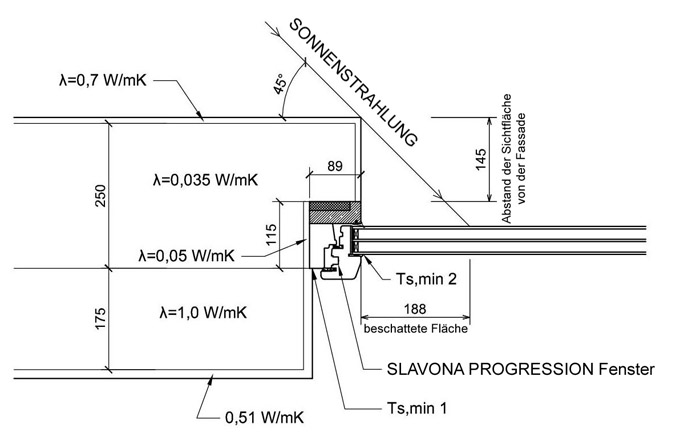
Abb.1: Skizze der Fensterlaibung, Kalksandsteine, Kontaktwärmedämmungssystem, Fenster PROGRESSION.
In der grafischen Darstellung 2 ist die Wärmebrücke in der Fensterlaibung (blau) und in der Brüstung (rot) abgebildet. Bei der Fensterlaibung erreicht die Wärmebrücke sowohl positive als auch negative Werte. Dies wird allgemein durch das Überziehen eines Wärmedämmstoffs über den Fensterrahmen verursacht. Gerade die Fenster des Typs Progression ermöglichen uns, den ganzen Fensterrahmen mit einem Wärmedämmstoff zu überziehen. Die kleinste Wärmebrücke entsteht hier, wenn sich die Einfassung des Fensterrahmens in einem Abstand von ca. 110 mm von Sichtfläche der Fassade befindet.
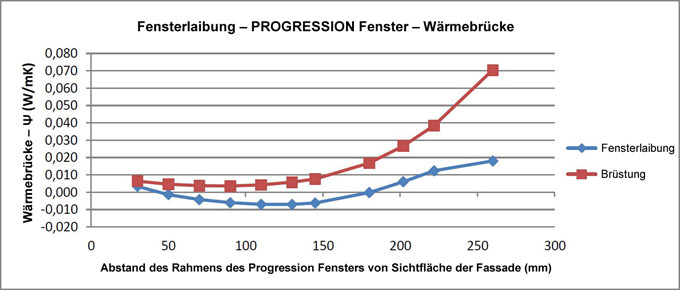
Abb. 2 Wärmebrücke in der Fensterlaibung und in der Brüstung.
Vergleich der Wärmebrücke und der Solargewinne
In Graph 3 kann man den Einfluss der Wärmebrücke und der Beschattung der Verglasung durch die Mauerecke sehen. In diesem Falle handelt sich es um ein Fenster des Typs PROGRESSION (Abmessungen des Fensters 1,2×1,5m). Beide Einflüsse sind in Watt aufgeführt, damit wir diese addieren und den idealen Abstand des Fensterrahmens von der Sichtfläche der Fassade bewerten können. Es ist klar, dass der Einfluss der Beschattung linear steigt. Was die Wärmebrücke betrifft, so ist diese am kleinsten, wenn sich das Fenster ungefähr 110 mm von Sichtfläche der Fassade befindet. Wenn beide Einflüsse addiert werden, werden die geringsten Verluste dann erreicht, wenn das Fenster 70 mm von Außensichtfläche der Fassade entfernt ist. Aber auch die anderen Werte sind fast identisch. Ein ähnliches Ergebnis wird erzielt, wenn das Fenster in einem Abstand von zirka 50mm bis 110mm von der Sichtfläche der Fassade eingefasst ist. Deshalb ist es erforderlich, die Vorteile dieser beiden Lösungen im Hinblick auf die Unkompliziertheit und die Durchführbarkeit von Details wie auch im Hinblick auf die architektonische Lösung abzuwägen.
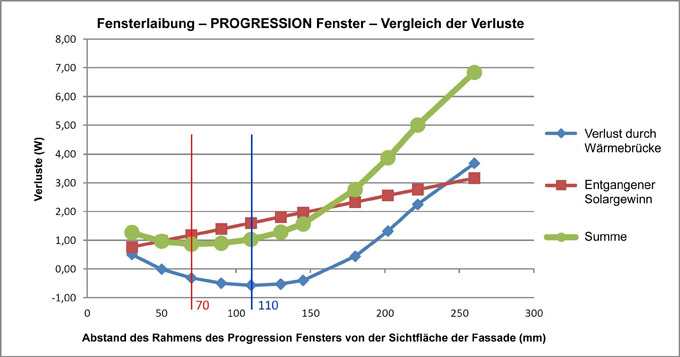
Abb. 3 Verluste – Wärmebrücke und verlorene Wärmegewinne. Werte siehe Tab. 2:
| Abstand des Fensters von Sichtfläche der Fassade* | mm | 30 | 50 | 70 | 90 | 110 | 130 | 145 | 180 | 202 | 222 | 260 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Ψ Fensterlaibung | W/(mK) | 0,003 | -0,001 | -0,004 | -0,006 | -0,007 | -0,007 | -0,006 | 0,000 | 0,006 | 0,012 | 0,018 |
| Ψ Brüstung | W/(mK) | 0,006 | 0,005 | 0,004 | 0,003 | 0,004 | 0,006 | 0,008 | 0,017 | 0,027 | 0,038 | 0,070 |
| Verlust durch Wärmebrücke** | W | 0,50 | -0,01 | -0,32 | -0,50 | -0,57 | -0,53 | -0,40 | 0,44 | 1,31 | 2,24 | 3,68 |
| Durch Mauerecke beschattete Fläche | m2 | 0,10 | 0,12 | 0,15 | 0,17 | 0,20 | 0,23 | 0,24 | 0,29 | 0,32 | 0,35 | 0,39 |
| Entgangener Solargewinn*** | W | 0,76 | 0,97 | 1,18 | 1,39 | 1,60 | 1,80 | 1,96 | 2,33 | 2,56 | 2,76 | 3,16 |
| Summe der Verluste (Ψ und Solar) | W | 1,26 | 0,96 | 0,86 | 0,89 | 1,03 | 1,28 | 1,56 | 2,76 | 3,87 | 5,01 | 6,84 |
| ts,min1 (Bauwerk) | °C | 17,27 | 17,52 | 17,73 | 17,92 | 18,14 | 18,41 | 18,61 | 18,66 | 18,57 | 18,48 | 18,37 |
| ts,min2 (Verglasung) | °C | 15,04 | 15,12 | 15,17 | 15,22 | 15,25 | 15,29 | 15,33 | 15,47 | 15,57 | 15,65 | 15,72 |
Anm.:
* 145mm – das Fenster ist auf Ebene der Wärmedämmung eingefasst (siehe Skizze). 260 mm – Die Außensichtfläche des Rahmens ist mit dem Mauerwerk bündig.
** Stellt die Summe der Wärmebrücken multipliziert mit Temperaturgradient dar: Verlust = Δt⋅Σ(Ψi⋅li); wobei Δt=23°C die Temperaturdifferenz des Interieurs und der durchschnittlichen Außenraumtemperatur im gegebenen Monat (Januar) ist. Fenster mit Breite 1,2m und Höhe 1,5m. (li sind die Längen der Wärmebrücken – also Brüstung 1,2m; Fensterlaibung 4,2m; die Wärmebrücke im Laibungsbogen wird als identisch mit der Fensterlaibung betrachtet)
*** Energie, die durch die beschattete Fläche in den Innenraum durchdringen würde, falls die Mauerecke nicht beschatten würde und die Strahlen auf die Verglasung einfallen würden E=8,01⋅SBeschattung durch Mauerecke
Oberflächentemperatur in der Fensterlaibung
Die Lage der Fenstereinfassung beeinflusst natürlich auch die Oberflächentemperatur. Die Oberflächentemperatur auf der Innenseite der Verglasung erhöht sich mit steigendem Abstand vom Außenraum, so dass es sich genau entgegengesetzt verhält, wie Wärmebrücke und Solargewinne. Je mehr das Fenster in die Wärmedämmung eingefasst wird, desto niedriger wird die Temperatur. Die Differenzen sind aber keineswegs dramatisch. In einem richtig genutzten, hochwertigen Haus mit hochwertigen Fenstern (wie z.B. PROGRESSION) kommt es nicht zur Oberflächenkondensation.
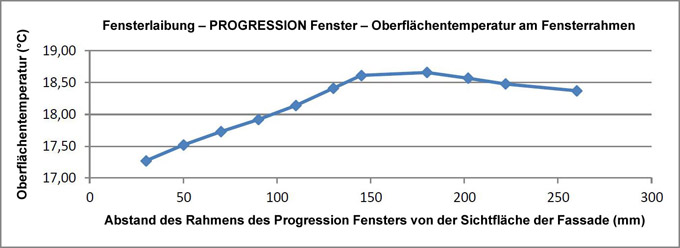
Abb. 4 Oberflächentemperatur an der Verbindungsstelle des Fensterrahmens und der Wand (bei der Anschlussfuge); ti=21°C, te=-15°C, zur Berechnung der Oberflächentemperaturen Rsi=0,25 m2K/W
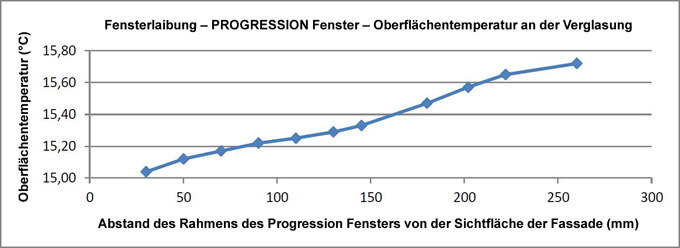
Abb. 5 Oberflächentemperatur an der Verbindungsstelle der Verglasung und des Fensterrahmens (bei der Verglasungsfuge); ti=21°C, te=-15°C, zur Berechnung der Oberflächentemperaturen Rsi=0,13 m2K/W.
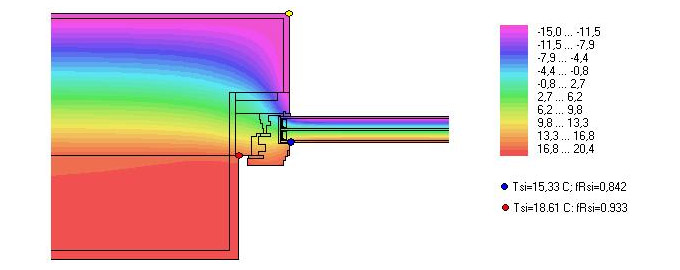
Abb. 6 Fensterlaibung – Temperaturfeld
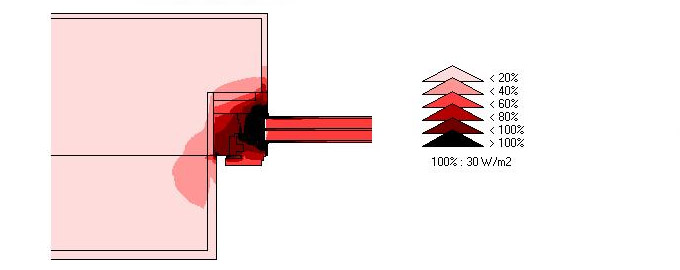
Abb. 7 Fensterlaibung – Verteilung der Wärmestromdichte. Die größte Wärme entweicht am Distanzrahmen, auch in diesem optimal gelösten Fall, in dem ein hochwertiger Swisspacer-V-Distanzrahmen eingesetzt wird.
Autor des Artikels: Ing. Jakub Hrdlička


